Flow to the Mode: Mode-Seeking Diffusion Autoencoders for State-of-the-Art Image Tokenization

Kyle Sargent¹, Kyle Hsu¹, Justin Johnson², Li Fei-Fei¹, Jiajun Wu¹,
Stanford University¹, University of Michigan²

Paper Code (coming soon!)

Gallery Links

Please check out our galleries (FlowMo-Lo gallery, FlowMo-Hi gallery) for more visual comparisons against baselines!

Introduction

Since the advent of popular visual generation frameworks like VQGAN and Latent Diffusion Models, state-of-the-art image generation systems have generally been two-stage systems that first tokenize or compress visual data into a lower-dimensional latent space before learning a generative model. Tokenizer training typically follows a standard recipe in which images are compressed and reconstructed subject to a combination of MSE, perceptual, and adversarial losses. Diffusion autoencoders have been proposed in prior work as a way to learn end-to-end perceptually-oriented image compression, but have not yet shown state-of-the-art performance on the competitive task of ImageNet1K reconstruction. In this work, we propose FlowMo, a transformer-based diffusion autoencoder. FlowMo achieves a new state-of-the-art for image tokenization at multiple bitrates. We achieve this without using convolutions, adversarial losses, spatially-aligned 2-dimensional latent codes, or distilling from other tokenizers. Our key insight is that FlowMo training should be broken into a mode-matching pre-training stage and a mode-seeking post-training stage. We conduct extensive analysis and ablations, and we additionally train generative models atop the FlowMo tokenizer and verify the performance.

Vector Graphic — Figure 1: When trained for reconstruction at a low bitrate (FlowMo-Lo) or high bitrate (FlowMo-Hi), FlowMo achieves state-of-the art image tokenization performance. Moreover, FlowMo is a transformer-based diffusion autoencoder which does not use convolutions, adversarial losses, or proxy objectives from auxiliary tokenizers.

Method

We'll briefly outline the architecture and training stages below. For an in-depth summary, check out our paper!

Architecture

FlowMo is implemented as a diffusion autoencoder with transformer-based encoder and decoder. The architecture diagram is shown below.

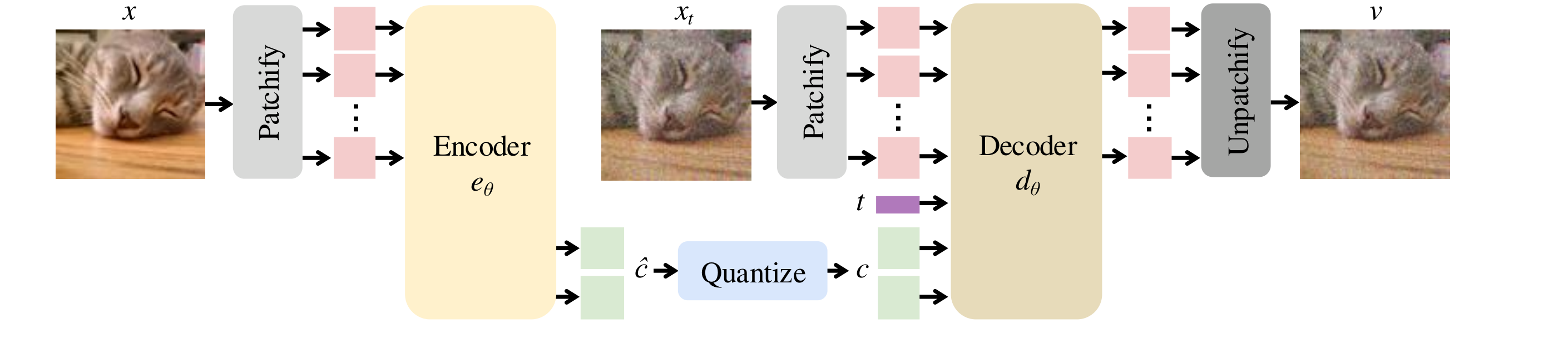
The encoder maps an image x (with an initial latent c₀) to a continuous latent representation:

\hat{c} = e_{\theta}(x, c_0)~,

which is quantized using lookup-free quantization, as

c = q(\hat{c}) = 2 \cdot \mathbf{1}[\hat{c} \geq 0] - 1~.

The decoder models a velocity field that transforms a noisy image back to a clean one. A noisy image x_t is defined as:

x_t = t \cdot z + (1 - t) \cdot x \quad \text{with} \quad z \sim \mathcal{N}(0, I), \quad t \in [0, 1] ~ .

The decoder then predicts:

v = d_{\theta}(x_t, c, t)~.

Mode-matching pre-training

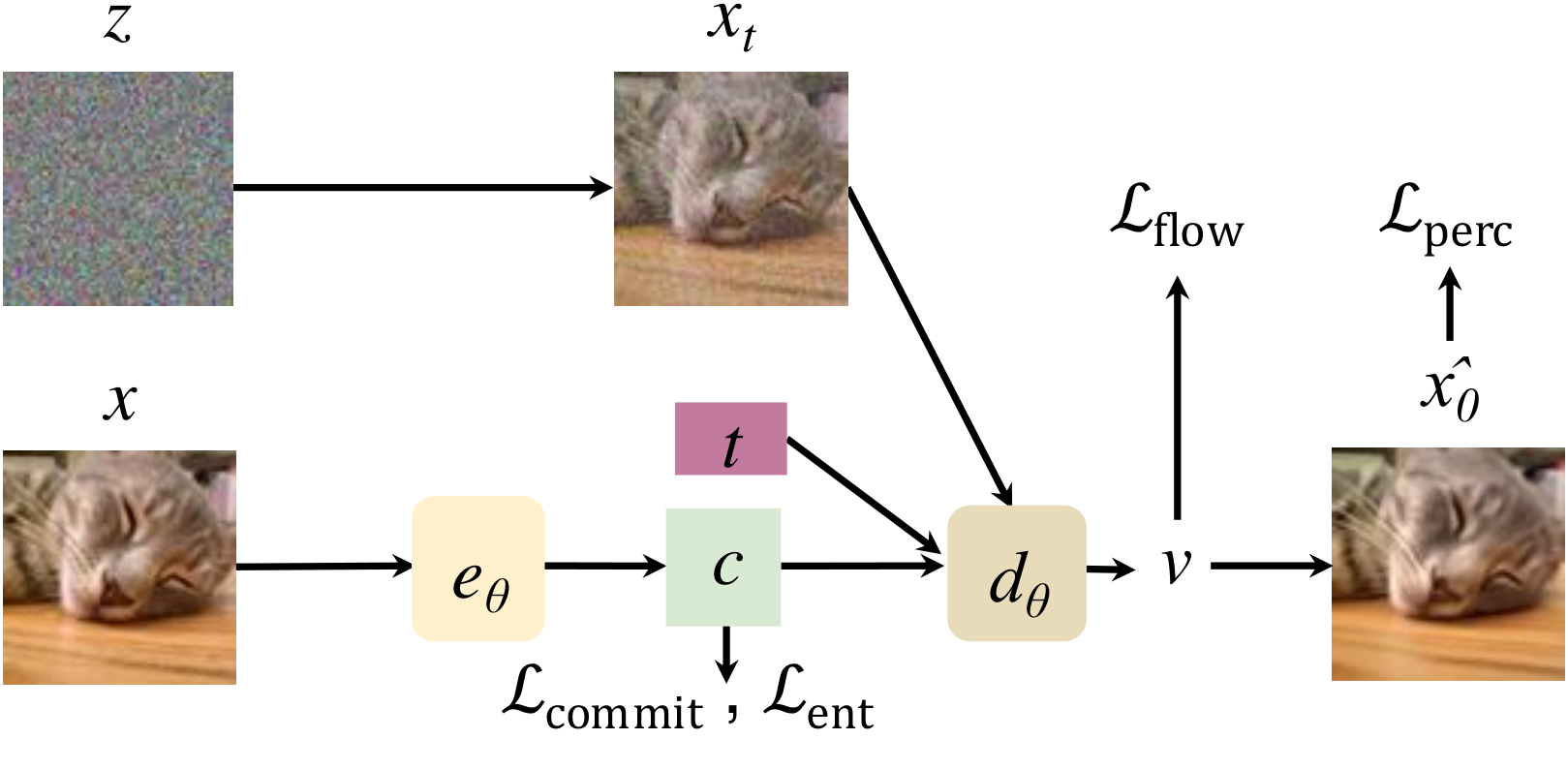
First, FlowMo is trained end-to-end as a diffusion autoencoder. A diagram of the Stage 1A training is shown below: Vector Graphic

The model is trained end-to-end with a diffusion loss

\mathcal{L}_{\text{flow}} = \mathbb{E}\Big[\big\|x - z - d_{\theta}(x_t, q(e_{\theta}(x)), t)\big\|_2^2\Big]~.

Additional losses include a perceptual loss \( \mathcal{L}_{\text{perc}} \) and quantization losses \( \mathcal{L}_{\text{commit}} \) and \( \mathcal{L}_{\text{ent}} \). The overall loss is:

\mathcal{L}_{\text{flow}} + \lambda_{\text{perc}} \mathcal{L}_{\text{perc}} + \lambda_{\text{commit}} \mathcal{L}_{\text{commit}} + \lambda_{\text{ent}} \mathcal{L}_{\text{ent}}~.

Mode-seeking post-training

In Stage 1B of training, the goal is to constrain the model to drop modes of the reconstruction distribution which are not perceptually close to the original image. A diagram is shown below:

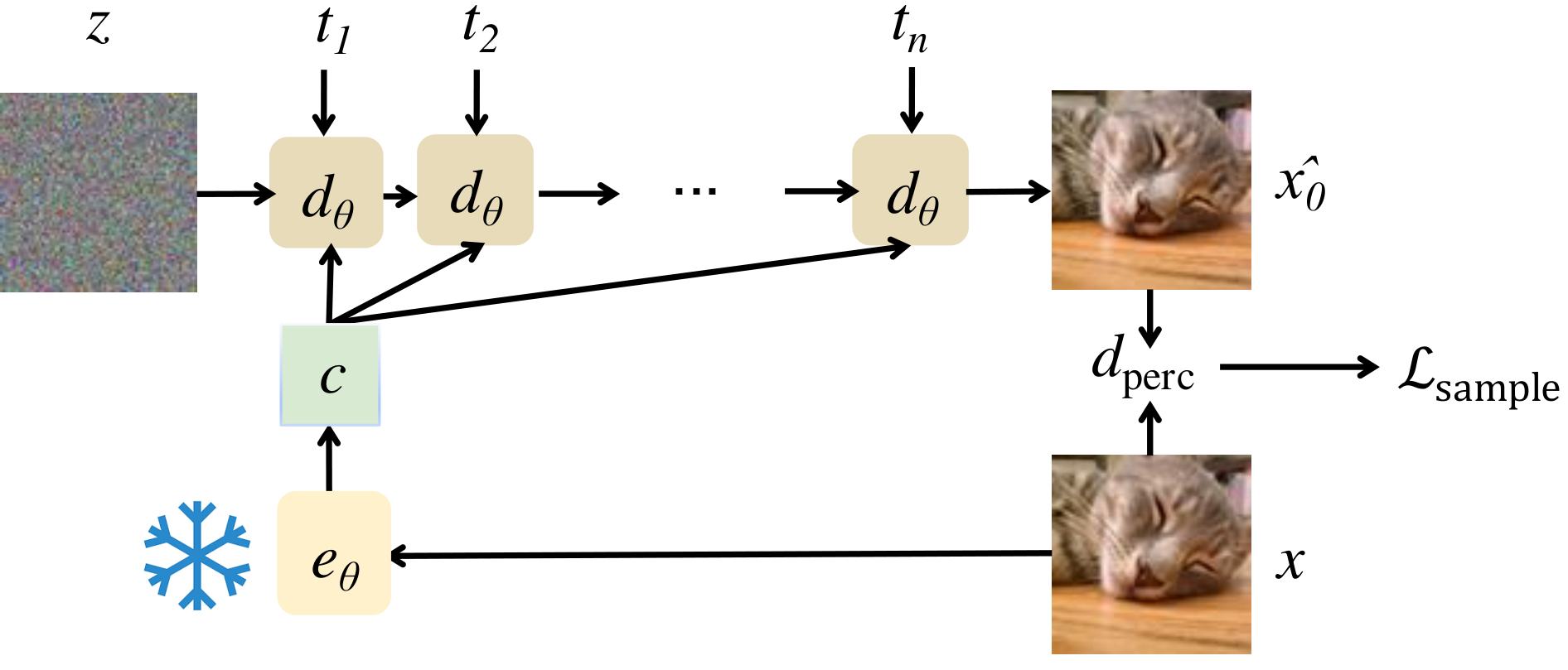
Vector Graphic

In this stage, the encoder is fixed and the decoder is fine-tuned using a sample-level perceptual loss:

\mathcal{L}_{\text{sample}} = \mathbb{E}\Big[d_{\text{perc}}\Big(x, \Big(d_{t_n} \circ d_{t_{n-1}} \circ \cdots \circ d_{t_1}\Big)(x)\Big]\Big)~.

The total loss during this stage becomes:

\mathcal{L}_{\text{flow}} + \lambda_{\text{sample}} \mathcal{L}_{\text{sample}}~.

Conclusion

Please check out our paper for detailed comparisons and analysis, and our galleries (FlowMo-Lo , FlowMo-Hi) for interactive comparisons. Stay tuned for code and checkpoints!

Citation

@misc{sargent2025flowmodemodeseekingdiffusion,
      title={Flow to the Mode: Mode-Seeking Diffusion Autoencoders for State-of-the-Art Image Tokenization}, 
      author={Kyle Sargent and Kyle Hsu and Justin Johnson and Li Fei-Fei and Jiajun Wu},
      year={2025},
      eprint={2503.11056},
      archivePrefix={arXiv},
      primaryClass={cs.CV},
      url={https://arxiv.org/abs/2503.11056}, 
}